近日,，計(jì)算機(jī)與信息學(xué)院PRiSE（Pattern Recognition and intelligence Software Engineering）研究團(tuán)隊(duì)盧桂馥教授指導(dǎo)的碩士研究生杜揚(yáng)帆在子空間聚類領(lǐng)域取得最新成果,，該成果發(fā)表在國(guó)際圖像處理領(lǐng)域頂級(jí)期刊“IEEE Transactions on Image Processing ”,。該期刊由美國(guó)電氣電子工程師學(xué)會(huì)（Institute of Electrical and Electronics Engineers,，IEEE）主辦,，是CCF A類期刊,、中科院SCI一區(qū)Top期刊,。該研究成果標(biāo)志我院碩士研究生教育取得新突破,。

針對(duì)子空間聚類問題,，該研究成果從多視圖聚類的角度出發(fā)并提供了相應(yīng)的解決方案,，首次提出了一種融合不同親和矩陣的方法。對(duì)于子空間聚類算法大多需要調(diào)節(jié)參數(shù)等問題,，假定由不同參數(shù)值產(chǎn)生的親和矩陣包含一致且互補(bǔ)的信息,，提出了一種新的魯棒最小二乘回歸方法（RLSR/MVCP）,。

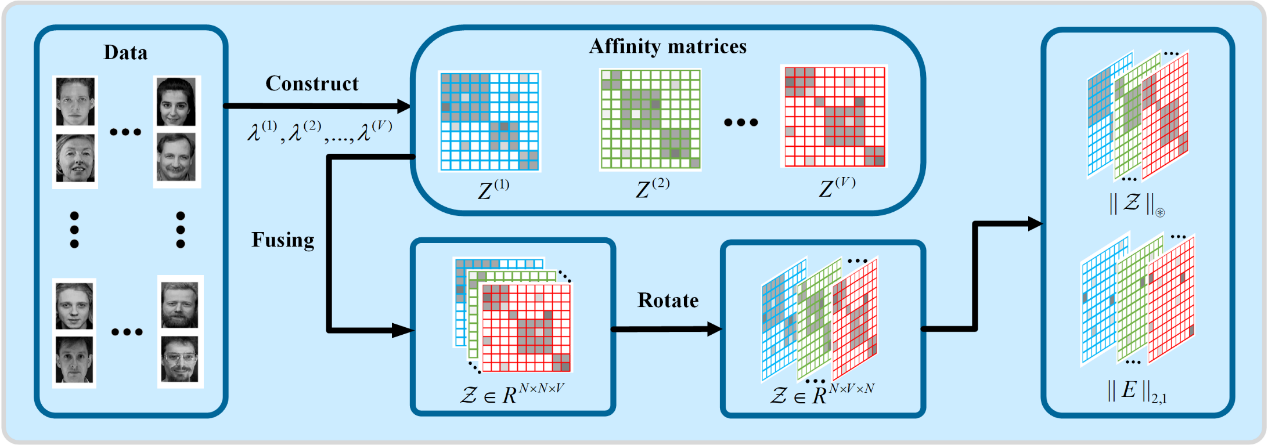
（RLSR/MVCP的整體框架流程圖）

具體來說，該研究首先使用具有不同參數(shù)值的LSR來獲得不同的親和矩陣,。然后,，為了充分探索這些親和矩陣中包含的信息并去除噪聲，將這些親和矩陣進(jìn)一步融合到張量中,，并對(duì)該張量施加張量低秩約束,。最后，將這兩個(gè)步驟融合到統(tǒng)一框架中,，并利用增廣拉格朗日乘子法（ALM）進(jìn)行優(yōu)化,。在數(shù)據(jù)集上的實(shí)驗(yàn)結(jié)果表明，RLSR/MVCP具有令人滿意的聚類性能,，并且優(yōu)于最先進(jìn)的子空間聚類方法,。該研究具有重要理論研究意義和實(shí)際應(yīng)用價(jià)值，為子空間聚類提供了一種嶄新的思路,。

近年來,，計(jì)算機(jī)與信息學(xué)院深度融合地方經(jīng)濟(jì)，積極推動(dòng)有組織科研,。PRiSE研究團(tuán)隊(duì)由王勇教授和盧桂馥教授牽頭組建于2020年,，現(xiàn)有教師8人，碩士研究生18人,。自2020年以來,，PRiSE研究團(tuán)隊(duì)主要圍繞模式識(shí)別和智能軟件工程的基礎(chǔ)理論和應(yīng)用開展研究，已發(fā)表SCI/EI收錄論文30余篇,，其中,，中科院一區(qū)以上論文10篇。研究團(tuán)隊(duì)已畢業(yè)碩士研究生10人,，其中,，4名研究生考取211高校博士研究生。

（文/圖：杜楊帆,；審核：王勇）